アタポンイベントにおけるpt調整

calendar 2023-12-17 · 3 分で読了 · シンデレラガールズ デレステ イベント攻略 Python  ·
共有する: bluesky mastodon2 misskey copy
イベント「幸せの法則 ～ルール～」 190101pt調整
イベント「幸せの法則 ～ルール～」 190101pt調整

目次

デレステでアタポン形式イベントのポイント数を調整したいと（2020年に）思ったので、調整ツールを作った。2020年なのでプロデュース方針や8倍消費など変わってる部分もあるが基本は同じ。サムネはほたるのボイス実装日が2019/01/01で01/01は茄子さんの誕生日でもあるので190101に合わせた画像。他にこの値に合わせた人はいなかったけど。

概要

イベントptをある設定した値に調整するにはどの曲を何回やればよいか検討する。ランダム要素があるため、営業、ぴにゃリクエスト、LIVE PARTY!!は考慮しないものとする。

立式

変数がとても多いので、まず楽曲プレイ回数の変数を下表に示す。ここで、\(n_{i\_j}\)はスタミナ\(i\)の通常楽曲を\(j\)倍消費でプレイする回数、\(e_{i\_j}\)はイベント楽曲を\(j\)倍消費でプレイする回数である。プロデュース方針で消費スタミナ軽減されている場合は調整が必要となる。

変数名 難易度 消費スタミナ 取得pt 取得アイテム数
\(n_{10\_1}\) DEB 10 25 25
\(n_{11\_1}\) DEB 11 28 28
\(n_{12\_1}\) REG 12 31 31
\(n_{13\_1}\) REG 13 34 34
\(n_{14\_1}\) REG 14 37 37
\(n_{15\_1}\) PRO 15 40 40
\(n_{16\_1}\) PRO 16 44 44
\(n_{17\_1}\) PRO 17 47 47
\(n_{18\_1}\) MAS 18 50 50
\(n_{19\_1}\) MAS 19 53 53
\(n_{25\_1}\) PNO 25 70 70
\(n_{30\_1}\) FOR 30 84 84
\(n_{10\_2}\) DEB 20 25 50
\(n_{11\_2}\) DEB 22 28 56
\(n_{12\_2}\) REG 24 31 62
\(n_{13\_2}\) REG 26 34 68
\(n_{14\_2}\) REG 28 37 74
\(n_{15\_2}\) PRO 30 40 80
\(n_{16\_2}\) PRO 32 44 88
\(n_{17\_2}\) PRO 34 47 94
\(n_{18\_2}\) MAS 36 50 100
\(n_{19\_2}\) MAS 38 53 106
\(n_{25\_2}\) PNO 50 70 140
\(n_{30\_2}\) FOR 60 84 168
\(e_{75\_1}\) DEB 0 130 -75
\(e_{90\_1}\) REG 0 170 -90
\(e_{120\_1}\) PRO 0 240 -120
\(e_{150\_1}\) MAS 0 320 -150
\(e_{75\_2}\) DEB 0 260 -150
\(e_{90\_2}\) REG 0 340 -180
\(e_{120\_2}\) PRO 0 480 -240
\(e_{150\_2}\) MAS 0 640 -300
\(e_{75\_4}\) DEB 0 520 -300
\(e_{90\_4}\) REG 0 680 -360
\(e_{120\_4}\) PRO 0 960 -480
\(e_{150\_4}\) MAS 0 1280 -600
\(e_{75\_8}\) DEB 0 1040 -600
\(e_{90\_8}\) REG 0 1360 -720
\(e_{120\_8}\) PRO 0 1920 -960
\(e_{150\_8}\) MAS 0 2560 -1200

多いのでベクトル化する。

$$\boldsymbol{n}_j =\left(\begin{array}{c}n_{10\_j} \cr n_{11\_j} \cr n_{12\_j} \cr n_{13\_j} \cr n_{14\_j} \cr n_{15\_j} \cr n_{16\_j} \cr n_{17\_j} \cr n_{18\_j} \cr n_{19\_j} \cr n_{25\_j} \cr n_{30\_j}\end{array}\right),\boldsymbol{e}_j =\left(\begin{array}{c}e_{75\_j} \cr e_{90\_j} \cr e_{120\_j} \cr e_{150\_j}\end{array}\right)$$

それ以外の変数を下表に示す。

変数名 意味
\(p_t\) 目標pt
\(p_c\) 現在pt
\(i_c\) 現在所持アイテム数
\(S\) 消費スタミナ
\(N\) 楽曲プレイ回数

ここから、求めるイベントptの関係は以下のようになる。取得イベントpt\(\times\)プレイ回数の合計と残り必要なイベントpt（\(=p_t - p_c\)）を一致させる。通常楽曲を2倍消費でプレイしてもイベントptは2倍にならない点に注意。

$$\left(\begin{array}{cccccccccccc}25 & 28 & 31 & 34 & 37 & 40 & 44 & 47 & 50 & 53 & 70 & 84\end{array}\right)\left(\boldsymbol{n}_1 + \boldsymbol{n}_2\right) \\+\left(\begin{array}{cccc}130 & 170 & 240 & 320\end{array}\right)\left(\boldsymbol{e}_1 + 2\boldsymbol{e}_2 + 4\boldsymbol{e}_4 + 8\boldsymbol{e}_8\right) = p_t - p_c $$

イベントアイテムの個数がマイナスになることはないので以下の式も成立する。

$$ i_c +\left(\begin{array}{cccccccccccc}25 & 28 & 31 & 34 & 37 & 40 & 44 & 47 & 50 & 53 & 70 & 84\end{array}\right)\left(\boldsymbol{n}_1 + 2\boldsymbol{n}_2\right) \\+\left(\begin{array}{cccc}-75 & -90 & -120 & -150\end{array}\right)\left(\boldsymbol{e}_1 + 2\boldsymbol{e}_2 + 4\boldsymbol{e}_4 + 8\boldsymbol{e}_8\right) \geq 0 $$

合計消費スタミナと楽曲プレイ回数は以下のようになる。

$$ S =\left(\begin{array}{cccccccccccc}10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 25 & 30\end{array}\right)\left(\boldsymbol{n}_1 + 2\boldsymbol{n}_2\right) \\N =\left(\begin{array}{cccccccccccc}1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\end{array}\right)\left(\boldsymbol{n}_1 + \boldsymbol{n}_2\right) \\+\left(\begin{array}{cccc}1 & 1 & 1 & 1\end{array}\right)\left(\boldsymbol{e}_1 + \boldsymbol{e}_2 + \boldsymbol{e}_4 + \boldsymbol{e}_8\right)$$

満たすべき条件

イベントptの式とイベントアイテムの式を同時に満たし、合計消費スタミナ\(S\)または合計楽曲プレイ回数\(N\)が最小になる楽曲プレイ回数\(\boldsymbol{n}_j,\boldsymbol{e}_j\)を求める。プレイ回数は非負整数なので整数線形計画問題として解ける。

Pythonによる計算

当時はMIPCLを使っていたが、現在入手困難だし新しいソルバーもあるみたいなので書き換えたほうがいいかもしれない。今はPySCIPOpt？

実行

PandasとMIPCLをインストールした状態でコマンドラインから実行する。目標イベントptと現在イベントpt、所持イベントアイテム数を入力するとどの曲を何回すればいいか計算してくれる。検算もしてくれる。

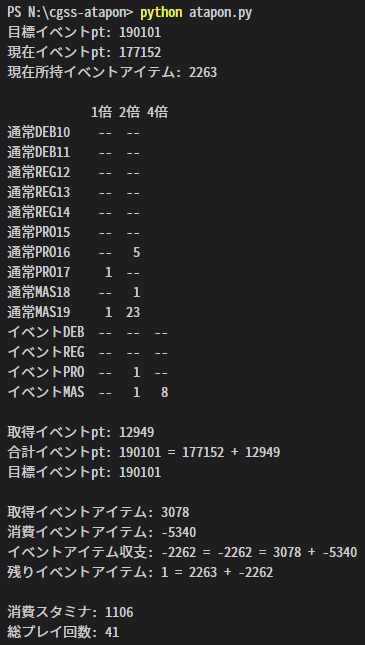
atapon.py実行結果

調整結果

2回ぐらい調整してみてそれぞれ成功した。

Hugo用のVSCode tasks.jsonを作成した Hugoに前後記事のリンクを追加する